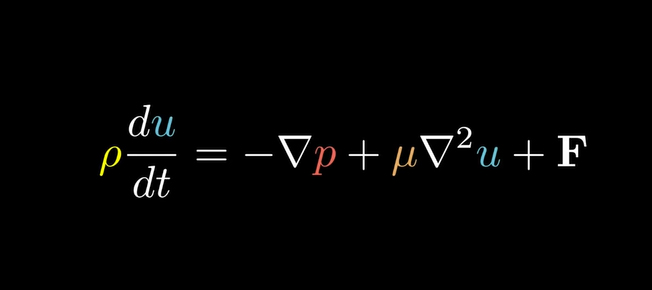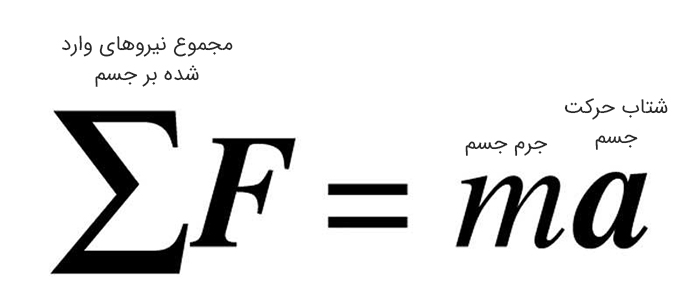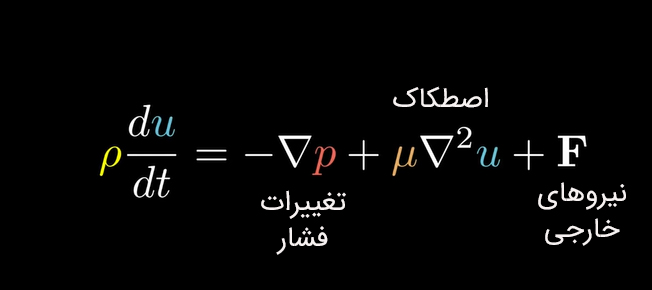تیمی متشکل از پژوهشگران و مهندسان، طی سه سال گذشته بهصورت محرمانه روی یکی از پیچیدهترین و چالشبرانگیزترین معماهای بشر کار کردهاند؛ معمایی که حل آن، سالها دور از دسترس بهنظر میرسید. اما اکنون، با پیشرفتهای چشمگیر در زمینه هوش مصنوعی، آنها بهنتایجی دست یافتهاند که نشان میدهد این قفل دیرینه، سرانجام در آستانه گشودهشدن قرار دارد.
خاویر گومس سرانو، ریاضیدان ۳۹ ساله اهل مادرید، با همکاری شرکت گوگل دیپمایند و هوش مصنوعی این شرکت، بهدنبال حل یکی از پیچیدهترین معادلات تاریخ بشر است: معادلات ناویه–استوکس (Navier–Stokes Equations). این معادلات که رفتار سیالات را توصیف میکند، یکی از هفت «مسئله جایزه هزاره» بهشمار میرود و مؤسسه ریاضی کلِی در آمریکا برای حل آنها یک میلیون دلار جایزه تعیین کرده است.
پروژهای که پژوهشگران آن را «عملیات ناویه–استوکس» نامیدهاند، طی سه سال گذشته در سکوت کامل و بدون جلب توجه عمومی جلو رفته است. حالا گمان میرود که منظور دمیس هسابیس، مدیرعامل دیپمایند، همین پروژه بوده باشد؛ و اگر همهچیز طبق پیشبینیها پیش برود، شاید ظرف یک سال یا یک سال و نیم آینده، بالاخره شاهد باز شدن یکی از بزرگترین قفلهای تاریخ ریاضیات باشیم؛ قفلی که قرنها دانشمندان را سردرگم نگه داشته بود.
معادلات ناویر–استوکس؛ زبان ریاضی برای توصیف حرکت سیال
فرض کنید کنار دریاچهای نشستهاید که آب بهآرامی در آن جریان دارد. اگر اطلاعات دقیقی از سرعت و فشار آب در هر نقطه از دریاچه داشته باشید، آیا میتوانید چگونگیِ جریان آب را در آینده پیشبینی کنید؟ این دقیقاً همان پرسشی است که ما را به سراغ معادلات ناویه–استوکس میبرد، مجموعهای از معادلات دیفرانسیل جزئی که رفتار هر نوع سیالی را توصیف میکنند، از آب و هوا تا روغن، عسل یا حتی گازها.
معادلات ناویه-استوکس یکی از بنیادیترین ابزارهای علمی برای فهم و مدلسازی پدیدههای فیزیکی هستند. از پیشبینی وضعیت آبوهوا تا طراحی هواپیما، شبیهسازی پرتاب موشک یا تحلیل جریان خون در رگها، همه بهنحوی به این معادلات وابسته هستند. با وجود کاربردهای گسترده در دنیای واقعی، هنوز از نظر ریاضی پرسشهای مهمی دربارهی آنها بیپاسخ ماندهاند: آیا این معادلات همیشه راهحل مشخص و قابلاعتمادی دارند و آیا رفتار آن همیشه آرام و پیوسته است؟ این همان چیزی است که در ریاضیات به آن «مسئلهی وجود و همواری» میگویند. همین پیچیدگیها باعث شده تا معادلات ناویه-استوکس در فهرست «مسائل جایزه هزاره» قرار گیرند که حل هر کدام یک میلیون دلار جایزه دارد.
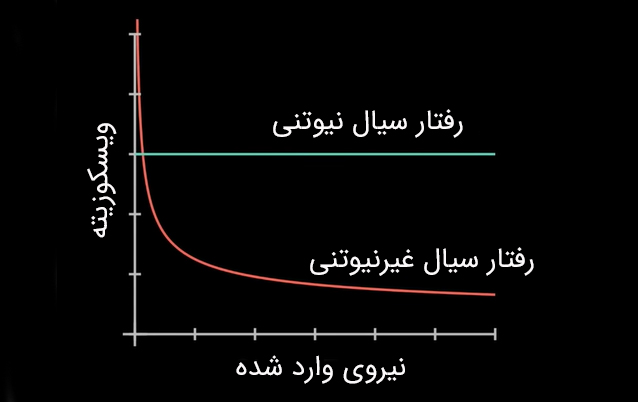
برای بررسی دقیقتر این معادلات، ابتدا باید چند فرض کلیدی را بپذیریم. یکی از مهمترین آنها این است که سیال موردنظر باید نیوتونی باشد.
اولین فرض برای نوشتن معادلات ناویر-استوکس: سیال نیوتنی
سیال نیوتونی سیالی است که ویسکوزیته (یا همان چسبندگیاش) مستقل از نیروی واردشده به آن، باقی میماند. به بیان سادهتر، اگر به چنین سیالی نیرو وارد کنیم، مقدار مقاومتش در برابر جاری شدن تغییر نمیکند. برای درک بهتر این مفهوم، به بطری سس فکر کنید؛ وقتی به ته آن ضربه میزنیم، سس ناگهان روان میشود. این نشان میدهد که سس یک سیال غیرنیوتونی است. در مقابل، سیالات نیوتونی مانند آب یا هوا، ویسکوزیته ثابت دارند و رفتارشان منظمتر و قابلپیشبینیتر است، به همین دلیل در معادلات ناویه-استوکس از آنها استفاده میشود.
دومین فرض برای نوشتن معادلات ناویر-استوکس: سیال تراکمناپذیر
فرض دوم آن است که سیال تراکمناپذیر باشد؛ یعنی اگر به آن فشار وارد کنیم، حجمش به طور قابلتوجهی تغییر نمیکند و چگالی آن تقریباً ثابت میماند. بسیاری از مایعات در شرایط عادی، مانند آب، تقریباً تراکمناپذیر در نظر گرفته میشوند و این فرض به سادهسازی معادلات کمک زیادی میکند.
سومین فرض برای نوشتن معادلات ناویر-استوکس: سیال همدما
فرض سوم نیز میگوید سیال، همدما یا ایزوترمال (Isothermal) است؛ یعنی دمای سیال در حین جریان ثابت باقی میماند. این فرض به ما اجازه میدهد بدون درگیر شدن با پیچیدگیهای انتقال حرارت، فقط روی رفتار حرکتی سیال تمرکز کنیم. با این سه فرض، اکنون میتوانیم سراغ معادلات ناویه–استوکس برویم. این معادلات بر پایه اصول شناخته شده فیزیک نوشته شدهاند: قانون بقای جرم (پیوستگی)، قانون دوم نیوتن (نیرو برابر است با جرم ضربدر شتاب) و قانون بقای تکانه. این معادلات رفتار هر واحد کوچکی از سیال را به دقت بررسی میکنند.
مفهوم واگرایی و نقش آن در معادله ناویر–استوکس
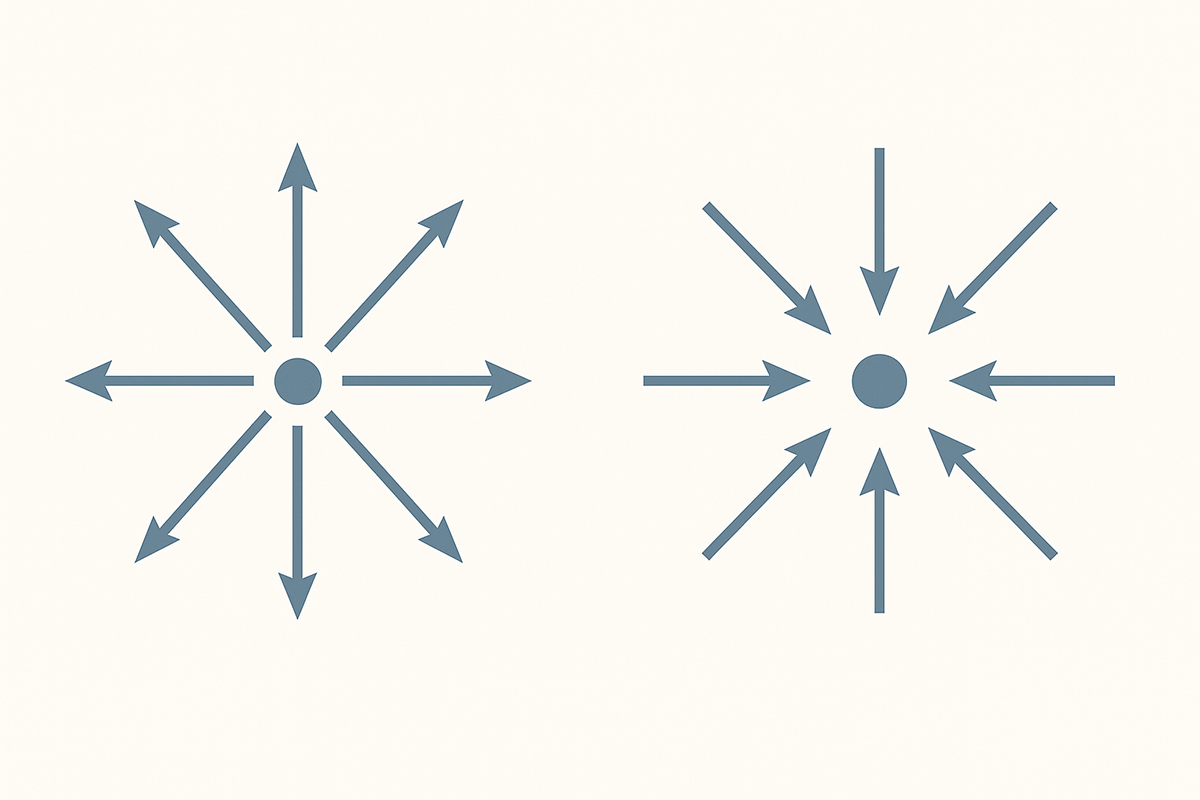
معادله اول ناویه–استوکس به ما میگوید که جرم سیال در گذر زمان ثابت میماند؛ یعنی هیچجایی در سیال نباید جرم بهطور ناگهانی ایجاد شود یا از بین برود. این مفهوم، همان اصل پایستگی جرم است که در زبان ریاضیات با عملگری به نام واگرایی (Divergence) بیان میشود.
در اینجا با یک میدان برداری به نام u روبهرو هستیم که در واقع همان میدان سرعت سیال است؛ یعنی در هر نقطه از فضا، یک بردار مشخص وجود دارد که هم جهت حرکت سیال و هم مقدار سرعت آن را نشان میدهد. واگرایی یک میدان برداری به ما نشان میدهد که بردارهای یک میدان در یک ناحیه از فضا چه رفتاری دارند: آیا تمایل دارند از آن نقطه دور یا به سمت آن جمع شوند. اگر بردارها از یک نقطه به اطراف پخش شوند، یعنی آن نقطه واگرایی مثبت دارد؛ درست مثل چشمهای که آب از دل آن به بیرون میجوشد. در مقابل، اگر همه بردارها به سمت یک نقطه کشیده و به آن نزدیک شوند، واگرایی منفی داریم؛ شبیه به یک حفره که همهچیز را به درون خودش میکشد.
در یک سیال تراکمناپذیر، واگرایی میدان سرعت باید حتماً صفر باشد. این دقیقاً همان چیزی است که معادله اول ناویه–استوکس به ما میگوید: در هیچجای سیال نباید نقطهای وجود داشته باشد که در آن، ماده بیدلیل ناپدید یا تولید شود.
معادله دوم ناویر-استوکس؛ قانون دوم نیوتن در دنیای سیالات
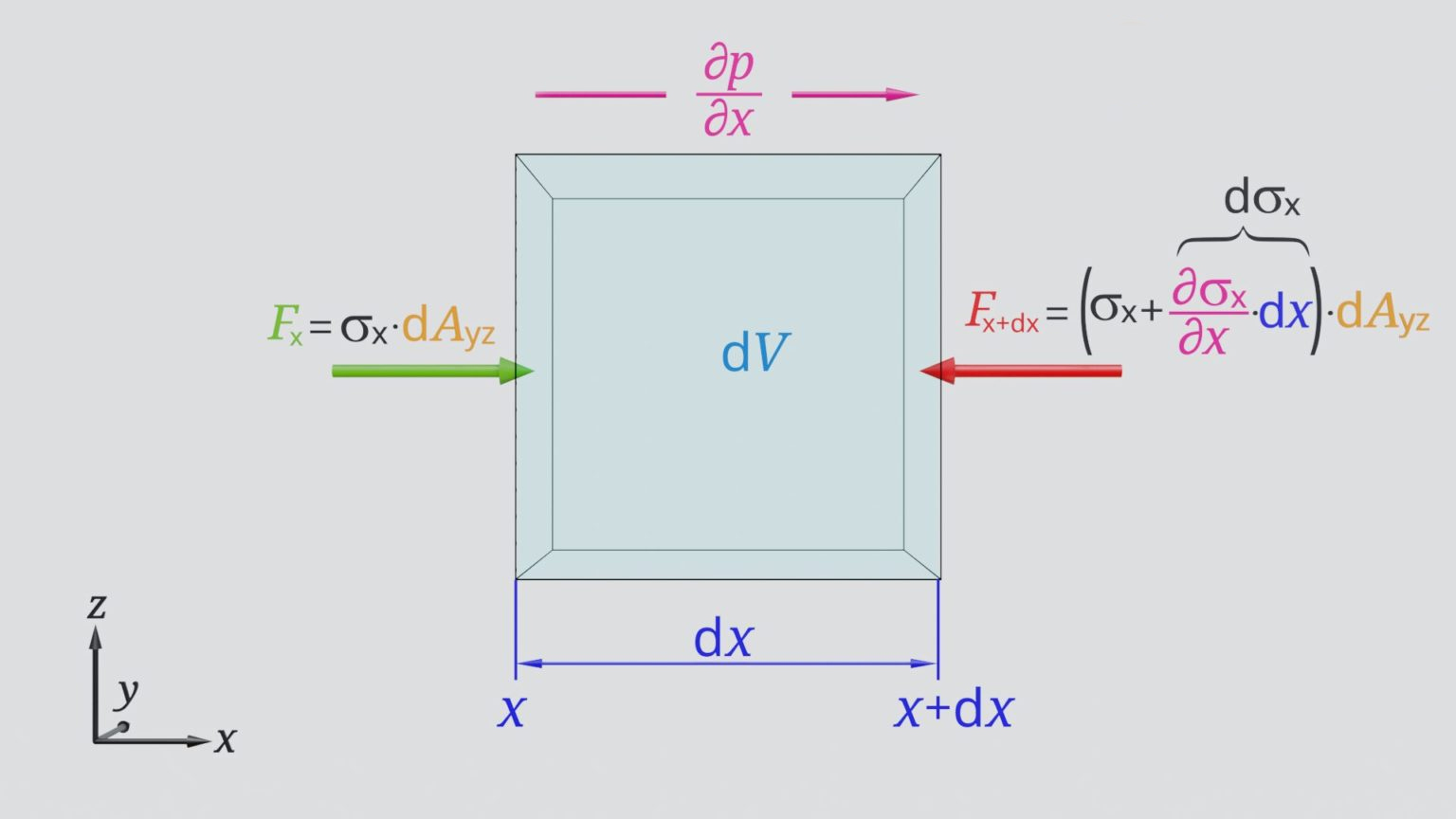
معادله دوم ناویه–استوکس در اصل همان قانون دوم نیوتن است که به زبانی جدید و برای سیالات نوشته شده است. این معادله مجموع نیروهای وارد بر یک بخش خیلی کوچک از سیال را برابر با جرم آن ضربدر شتابش میداند. به جای جرم، از چگالی استفاده میشود تا تحلیل رفتار سیال در هر نقطه دقیقتر باشد.
شتاب در معادلات سیالات فقط به تغییرات سرعت در یک نقطه محدود نمیشود؛ بلکه شامل تغییر سرعت در گذر زمان در یک نقطهی مشخص و تغییر سرعت به دلیل حرکت خود سیال از نقطهای به نقطهی دیگر است. با ترکیب این دو بخش، به شتاب کامل ذرهی سیال دست پیدا میکنیم.
تمام نیروهای وارد بر این نقطه کوچک از سیال شامل فشار، ویسکوزیته (اصطکاک داخلی سیال) و نیروهای خارجی مانند گرانش هستند. نیروی فشار با گرادیان فشار، ویسکوزیته با فرمولی خاص برای سیالات نیوتونی و گرانش با ضرب چگالی در شتاب گرانشی نمایش داده میشوند.
در مجموع، معادله دوم ناویه–استوکس همه نیروهایی را که بر یک نقطه از سیال وارد میشوند، ترکیب میکند تا نشان دهد که هر ذره از سیال دقیقاً چرا و چطور حرکت میکند. این معادلات پایهی شبیهسازیهای جریان هوا در اطراف هواپیما و خودروها را تشکیل میدهند و ستون فقرات پیشبینیهای هواشناسی به شمار میروند.
چالش بزرگ: پیچیدگی و همواری معادلات ناویر-استوکس
دلیل اینکه معادلات ناویه–استوکس میتوانند تقریباً هر نوع سیالی را مدلسازی کنند، به ترکیب دقیق قوانین بنیادی فیزیک در آنها باز میگردد. این معادلات میتوانند تغییرات سرعت، فشار و چگالی را در هر نقطه از سیال، در طول زمان توصیف کنند و انعطافپذیری بالایی در توصیف انواع جریانهای آرام تا آشفته دارند.
اما چرا حل این معادلات یک میلیون دلار جایزه دارد؟ مسئله اصلی به «راهحلهای هموار» (smooth solutions) برمیگردد؛ راهحلهایی که پیوسته و مشتقپذیر باشند و هیچ ناهمواری یا جهشی نداشته باشند. با این حال، رفتار سیالات واقعی به شدت آشفته است؛ کوچکترین تغییر در شرایط اولیه میتواند به تغییرات بزرگ و غیرقابلپیشبینی منجر شود، مانند اثر پروانهای در نظریه آشوب.
این آشفتهبودن پیشبینی رفتار بلندمدت سیالات را دشوار میکند، مانند پیشبینی دقیق آبوهوا. معمای ناویه–استوکس پرسشی بنیادین دربارهی پیشبینیپذیری و رفتار پیچیده سیالات در دنیای واقعی است. با گذشت حدود دو قرن از معرفی این معادلات، هنوز یک پرسش بنیادین بیپاسخ مانده است: آیا این معادلات همیشه راهحلی منظم و قابلپیشبینی دارند؟
خاویر گومس سرانو، رهبر تیمی از پژوهشگران، برای نخستین بار بهصورت عمومی دربارهی این تلاش بلندپروازانه صحبت کرده است. او معتقد است که در جامعه علمی نوعی اجماع به وجود آمده که حل این مسئله نزدیک است. در سال ۲۰۱۴، تیمی به رهبری توماس هو در کالیفرنیا با سادهتر کردن مسئله و استفاده از معادلات اویلر (نسخه بدون اصطکاک ناویه-استوکس)، به پیشرفت چشمگیری دست یافتند و پدیدهای شبیه به «تکینگی» (Singularity) را نشان دادند. در ادامه، تیم خاویر گومس با بهرهگیری از هوش مصنوعی، تکینگی را با دقت بسیار بالاتری مورد بررسی قرار داد و به نتایجی دست یافت که نشان میدهد حل این معما دور از دسترس نیست.
سرانو با صراحت میگوید: «مسئله ناویه–استوکس فوقالعاده دشوار است. ریاضیدانها سالها تلاش کردهاند، اما روشهای کلاسیک تا الان جواب ندادهاند.» به گفته او، استفاده از هوش مصنوعی استراتژی متمایز تیمش است و او خوشبین است که راهحل طی پنج سال آینده پیدا خواهد شد.
هوش مصنوعی در حل مسائل ریاضی: AlphaEvolve
خاویر گومس سرانو در پروژهی AlphaEvolve با گوگل دیپمایند مشارکت داشته است. AlphaEvolve یک سامانهی هوش مصنوعی کاملاً نوآورانه است که میتواند مسائل پیچیده ریاضی را با کارایی بیسابقه حل کند. این سیستم با آموزش روی ۵۰ مسئله دشوار، الگوهای ریاضی را یاد میگیرد و راهحلهایی پیشنهاد میدهد که گاهی حتی از روشهای سنتی هم بهتر است. گومس سرانو میگوید: «در ۷۵ درصد موارد، AlphaEvolve به همان پاسخی میرسد که بهترین ریاضیدانان انسان پیدا کردهاند. در ۲۰ درصد دیگر، حتی عملکرد بهتری دارد.»
چیزی که AlphaEvolve را به انقلابی تازه در هوش مصنوعی تبدیل میکند، این است که برخلاف برنامههای تخصصی مانند AlphaFold2، این سامانه یک مدل زبانی گسترده است که میتواند مسائل متنوعی را در شاخههای مختلف ریاضیات حل کند، بینیاز از آموزش تخصصی یا دادههای محدود. همین توانایی درک و حل مسئله در زمینههای گوناگون، آن را به ابزاری قدرتمند و انعطافپذیر در دنیای علم تبدیل کرده است.
دمیس هسابیس، مدیر دیپمایند، پیشبینی کرده است که «هوش عمومی مصنوعی» تا حدود سال ۲۰۳۰ ظهور خواهد کرد. خاویر گومس سرانو نیز سرعت پیشرفت را حیرتانگیز میداند و باور دارد که هوش مصنوعی دنیا را به سوی بهتر شدن تغییر خواهد داد.
منبع: Zoomit.ir